
Eccoci di nuovo qui dopo una breve pausa (causa esame di Sistemi di Controllo (mentale della popolazione) a Più Variabili). Nell'ultimo articolo relativo alla modellistica del comportamento di una particella singola avevamo alla fine di tutto elaborato un modello completo del comportamento di una particella immersa in un fluido incomprimibile con un flusso laminare.
Ora non resta che mettere insieme i risultati ricavati ed esposti nei vari articoli, e infilarli tutti nel modellino originario per potersene avvalere in fase di simulazione.
Ricordiamo per praticità che il modello in questione è definito dalla seguente:
Ora non resta che mettere insieme i risultati ricavati ed esposti nei vari articoli, e infilarli tutti nel modellino originario per potersene avvalere in fase di simulazione.
Ricordiamo per praticità che il modello in questione è definito dalla seguente:
m_{p}\frac{dv_{z}}{dt}=\frac{6\pi \mu(T(z)) R_{eq}\chi}{C_{c}(R_{eq})}\cdot (u_{z}-v_{z})+
V_{p}\rho(z,T(z))\frac{d u_{z}}{dt}+\frac{V_{p}}{2}\rho(z,T(z))\left(\frac{d u_{z}}{dt}-\frac{d v_{z}}{dt}\right)+
+6R_{eq}^{2}\sqrt{\pi\mu(T(z)) \rho(z,T(z))}\int\limits_{0}^{t}{\frac{\frac{du_{z}}{d\tau}-\frac{dv_{z}}{d\tau}}{\sqrt{t-\tau}}d\tau}+\sum\limits_{i}Fe_{i}
con μ viscosità del mezzo, ρ densità del mezzo, Cc Slip Correction Factor, Req il raggio equivalente della particella, mp massa della particella (considerando il galleggiamento), Vp volume della particella, uz velocità del vento lungo l'asse z, vz velocità della particella lungo l'asse z, T temperatura del mezzo e χ il fattore dinamico di forma.
Arrivati a questo punto, abbiamo precedentemente ricavato ed enunziato ogni relazione possibile per poter calcolare i parametri della formula a partire da pressione, temperatura ed umidità relativa. Ci si basa su queste grandezze perchè sono quelle di maggior interesse fornite dalle misurazioni delle sonde metereologiche, dal mommento che l'intenzione è quella di operare una simulazione numerica in un ambiente che abbia dei profili di pressione, umidità relativa e temperatura reali e non approssimati ai minimi termini (anche se le cose variano veramente di poco).
Iniziando dai parametri più semplici, vediamo che per ottenere la viscosità μ, basta usare la relazione di Sutherland:
Arrivati a questo punto, abbiamo precedentemente ricavato ed enunziato ogni relazione possibile per poter calcolare i parametri della formula a partire da pressione, temperatura ed umidità relativa. Ci si basa su queste grandezze perchè sono quelle di maggior interesse fornite dalle misurazioni delle sonde metereologiche, dal mommento che l'intenzione è quella di operare una simulazione numerica in un ambiente che abbia dei profili di pressione, umidità relativa e temperatura reali e non approssimati ai minimi termini (anche se le cose variano veramente di poco).
Iniziando dai parametri più semplici, vediamo che per ottenere la viscosità μ, basta usare la relazione di Sutherland:
\mu = 18.27\cdot 10^{-8}\frac{411.15}{T(z)+120}\sqrt{\left(\frac{T(z)}{291.15}\right)^{3}}
Qui non c'è molto da aggiungere, dal momento che basta sostituire la temperatura all'altezza z, e si ricava banalmente la viscosità dell'aria all'altrzza z.
Per la densità c'è da macchinare un poco con il vapore e le formule di Van der Waals, infatti occorre risolvere le seguenti due equazioni di terzo grado (indipendenti) rispettivamente per ρa e ρv:
Per la densità c'è da macchinare un poco con il vapore e le formule di Van der Waals, infatti occorre risolvere le seguenti due equazioni di terzo grado (indipendenti) rispettivamente per ρa e ρv:
\left(p(z)-e(z,T)\cdot u(z)+a\frac{\rho_{a}^{2}}{M^{2}}\right)\cdot(1-\frac{\rho_{a}}{M}\cdot b)=\rho_{a}\frac{R}{M}T
con b = 3.64·10^(-5)[m³/mol] ed a = 0.001358 [hPa (m^6)/mol²] e:
\left(e(z,T)\cdot u(z)+a\frac{\rho_{v}^{2}}{M^{2}}\right)\cdot(1-\frac{\rho_{v}}{M}\cdot b)=\rho_{v}\frac{R}{M}T
con b = 30.52·10^(-6)[m³/mol] ed a = 0.005536 [hPa (m^6)/mol²] ed e(z,T) definito dal modello di Murhpy-Koop:
\log(100\cdot e) = 54.842763 - \frac{6763.22}{T(z)} - 4.21\cdot\log(T(z))+ 0.000367T(z) + \tanh{(0.0415(T(z) - 218.8))}\cdot(53.878 - \frac{1331.22}{T(z)} - 9.44523\cdot\log(T(z)) + 0.014025 T(z))
che formulato in questo modo fornisce la pressione di saturazione del vapore sull'acqua in [hPa] a partire da una temperatura in [K].
La densità cercata, quella da mettere nell'equazione differenziale per il moto della particella sarà data dalla somma dei sue risultati trovati (ρa + ρv = ρ(z)).
Fin qui nessun problema, nè numerico, nè analitico (le formule esplicite per le radici di un'equazione di terzo grado esistono anche se sono un po' complicate). Unica accortezza per chi volesse usare le formule esplicite: innanzitutto assicuratevi di usare la soluzione giusta (quella positiva), secondo tutto attenzione all'ordine in cui mettete le numerose operazioni (potreste aver bisogno di rigirarvi un po' la formula) cercando di minimizzare la propagazione dell'errore. In questo caso basta un metodo di Newton-Raphson non ammortizzato per avere una buona e veloce convergenza.
Ora ultimo ma non per importanza il Cc. Dall'analisi del moto Browniano di una particella, abbiamo ricavato in quest'articolo una relazione tra lo Slip Correction Factor ed il cammino libero medio:
La densità cercata, quella da mettere nell'equazione differenziale per il moto della particella sarà data dalla somma dei sue risultati trovati (ρa + ρv = ρ(z)).
Fin qui nessun problema, nè numerico, nè analitico (le formule esplicite per le radici di un'equazione di terzo grado esistono anche se sono un po' complicate). Unica accortezza per chi volesse usare le formule esplicite: innanzitutto assicuratevi di usare la soluzione giusta (quella positiva), secondo tutto attenzione all'ordine in cui mettete le numerose operazioni (potreste aver bisogno di rigirarvi un po' la formula) cercando di minimizzare la propagazione dell'errore. In questo caso basta un metodo di Newton-Raphson non ammortizzato per avere una buona e veloce convergenza.
Ora ultimo ma non per importanza il Cc. Dall'analisi del moto Browniano di una particella, abbiamo ricavato in quest'articolo una relazione tra lo Slip Correction Factor ed il cammino libero medio:
\lambda_{p} = \frac{C_{c}}{6\mu}\sqrt{\frac{2\rho k T R_{p}}{3}}
Ancora prima però in quest'altro articolo avevamo proposto una formulazione dello Slip Correction Factor in funzione del cammino libero medio:
C_{c}=1+\frac{\lambda}{R_{p}}\left[1.257+0.4\cdot e^{-\frac{1.1R_{p}}{\lambda}}\right]
Sostituento la prima relazione nella seconda otteniamo:
C_{c}=1+\frac{\frac{C_{c}}{6\mu}\sqrt{\frac{2\rho k T R_{p}}{3}}}{R_{p}}\left[1.257+0.4\cdot e^{-\frac{1.1R_{p}}{\frac{C_{c}}{6\mu}\sqrt{\frac{2\rho k T R_{p}}{3}}}}\right]
Ora questa brutta bestia di equazione in Cc sfido chiunque a risolversela a mano ed a tirare fuori un'espressione esplicita per Cc. Fortuna nostra che tutti o quasi abbiamo un pc che fa il lavoro per noi in modo numerico. Ora questa stronza di equazione se non si prendono le dovute precauzioni manda in pappa (non lo fa convergere dove vogliamo noi) il nostro adorato metodo di Newton-Rahpson. Innanzitutto se lo si fa girare con un risolutore commerciale (MATLAB, Mpale, Mathematica) occorre stringere assai le tolleranze rispetto ai valori di default: per esempio per MATLAB qualcosa come 10^(-16) rispetto al 10^(-6) di default. Sostanzialmente questi numeretti dicono una serie di cose all'algoritmo:
1) quanto deve essere piccola la funzione per poter dire che vale effettivamente zero e terminare la ricerca dello zero della funzione;
2) quanto deve essere piccola la variazione per passo dell'algoritmo, dello zero che si sta trovando, per poter dire che ormai ci si sta stabilizzando ad un valore, e che quindi non vale la pena di continuare ad iterare, perchè tanto il valore di cui già si dispone non cambierà più di tanto.
Ricordo per semplicità che il metodo di Newton-Raphson classico per la risoluzione del problema f(x) = 0, è impostato come segue:
1) quanto deve essere piccola la funzione per poter dire che vale effettivamente zero e terminare la ricerca dello zero della funzione;
2) quanto deve essere piccola la variazione per passo dell'algoritmo, dello zero che si sta trovando, per poter dire che ormai ci si sta stabilizzando ad un valore, e che quindi non vale la pena di continuare ad iterare, perchè tanto il valore di cui già si dispone non cambierà più di tanto.
Ricordo per semplicità che il metodo di Newton-Raphson classico per la risoluzione del problema f(x) = 0, è impostato come segue:
x(0) = x_{0}
x_{n+1}=x_{n}-\frac{f(x_{n})}{f'(x_{n})}
dove f'(xn) è la derivata rispetto a x di f(x), calcolata in xn, ed x0 è ovviamente è la stima iniziale dello zero della funzione, per il contro caso del Cc è buona cosa metterlo pari ad 1.
Altra accortezza (che però non necessariamente è da mettere in pratica) è la valutazione dello Jacobiano (derivata della funzione se stiamo nel caso monodimensionale): spesso i metodi iterativi per la risoluzione di equazioni, per andare un po' più veloci e fare meno conti risparmiano sul calcolo della derivata. Insomma per più di qualche passo molti algoritmi sostanzialmente non ricalcolano la derivata della funzione e continuano ad usare il valore trovato qualche iterazione fà. Questa però è un'arma a doppio taglio:
1) Dal momento che non dobbiamo far girare il risolutore da solo fine a sè stesso ma dobbiamo integrare il tutto in un risolutore numerico di equazioni differenziali (un sacco di altre iterazioni e conti), per ogni passo di integratore numerico, occorrerà fare x passi del metodo di Newton, quindi se facciamo meno calcoli per ogni passo, alla fine la simulazione ci metterà molto di meno, quindi è buona cosa (se si può) evitare di calcolarsi la derivata ad ogni passo.
2) Se non calcoliamo la derivata ad ogni passo potremmo perdere in precisione, cosa questa, non certo auspicabile.
Pertanto occorrerebbe trovare un buon compromesso tra le due specifiche contrastanti, specialmente se il risolutore numerico utilizzato è già un po' pesantello di suo.
Vediamo un po' ora che cosa succede setralasciamo gradienti di pressione e tutte le altre schifezze che ci sono nel modello e ci limitiamo a simulare:
Altra accortezza (che però non necessariamente è da mettere in pratica) è la valutazione dello Jacobiano (derivata della funzione se stiamo nel caso monodimensionale): spesso i metodi iterativi per la risoluzione di equazioni, per andare un po' più veloci e fare meno conti risparmiano sul calcolo della derivata. Insomma per più di qualche passo molti algoritmi sostanzialmente non ricalcolano la derivata della funzione e continuano ad usare il valore trovato qualche iterazione fà. Questa però è un'arma a doppio taglio:
1) Dal momento che non dobbiamo far girare il risolutore da solo fine a sè stesso ma dobbiamo integrare il tutto in un risolutore numerico di equazioni differenziali (un sacco di altre iterazioni e conti), per ogni passo di integratore numerico, occorrerà fare x passi del metodo di Newton, quindi se facciamo meno calcoli per ogni passo, alla fine la simulazione ci metterà molto di meno, quindi è buona cosa (se si può) evitare di calcolarsi la derivata ad ogni passo.
2) Se non calcoliamo la derivata ad ogni passo potremmo perdere in precisione, cosa questa, non certo auspicabile.
Pertanto occorrerebbe trovare un buon compromesso tra le due specifiche contrastanti, specialmente se il risolutore numerico utilizzato è già un po' pesantello di suo.
Vediamo un po' ora che cosa succede setralasciamo gradienti di pressione e tutte le altre schifezze che ci sono nel modello e ci limitiamo a simulare:
\frac{dv_{z}}{dt}=-\frac{(6\pi\mu \cdot R_{eq}\Chi)}{(C_{c} V_{p} (\rho_{p}-\rho_{a}))}\cdot (v_{z}-u_{z})-g;
In questo caso si è scelto l'asse z positivo verso l'alto (opposto rispetto alla formulazione originaria, ma per rimediare basta cambiare il segno a v ed a dv/dt)
con condizioni iniziali v0=-60 [m/s] (verso il basso), z0=5000 [m] ed uz=6 [m/s].
Uniche due accortezze prima di lanciarci nella simulazione:
1) Usare un metodo di integrazione implicito (se usate MATLAB ode23tb, o un'altro risolutore per problemi stiff) come per esempio i vari Runge-Kutta impliciti (quadrature di Radau e Lobatto) o eulero implicito, o metodo dei trapezi implicito, perchè a causa della grande variazione della velocità iniziale in tempi brevissimi, i metodi espliciti (per chi usa MATLAB ode45 et similia) con passo di integrazione adattativo, tendono ad inchiodare velocemente ed all'inizio, e risultano quindi inutilmente lenti.
2) Riportare l'equazione differenziale del secondo ordine ad un sistema del primo ordine, facendo la sostituzione dz/dt = v, per ottenere invece della prima equazione, le due equazioni seguenti:
con condizioni iniziali v0=-60 [m/s] (verso il basso), z0=5000 [m] ed uz=6 [m/s].
Uniche due accortezze prima di lanciarci nella simulazione:
1) Usare un metodo di integrazione implicito (se usate MATLAB ode23tb, o un'altro risolutore per problemi stiff) come per esempio i vari Runge-Kutta impliciti (quadrature di Radau e Lobatto) o eulero implicito, o metodo dei trapezi implicito, perchè a causa della grande variazione della velocità iniziale in tempi brevissimi, i metodi espliciti (per chi usa MATLAB ode45 et similia) con passo di integrazione adattativo, tendono ad inchiodare velocemente ed all'inizio, e risultano quindi inutilmente lenti.
2) Riportare l'equazione differenziale del secondo ordine ad un sistema del primo ordine, facendo la sostituzione dz/dt = v, per ottenere invece della prima equazione, le due equazioni seguenti:
\left\{ \begin{array}{l}
\frac{\displaystyle dv_{z}}{\displaystyle dt}=-\frac{\displaystyle (6\pi\mu(z) \cdot R_{eq}\Chi)}{\displaystyle (C_{c}(z) V_{p} (\rho_{p}-\rho_{a}(z)))}\cdot (v_{z}-u_{z})-g\\
\\
\frac{\displaystyle dz}{\displaystyle dt}=v_{z}
\end{array} \right.
Ora mettendo dentro vari numeretti, ci possiamo fare le nostre simulazioni (tralasciando per ora la forza di Basset, il gradiente di pressione e la massa apparente della particella) ottenendo i seguenti risultati:
Per le velocità :
Per le velocità :

e per le posizioni:

Con gli zoom delle regioni di interesse per le due grandezze:
Per le velocità:

e per le posizioni:

Come si può vedere dalle legende, sono stati simulati i comportamenti di varie schifezze, le cui particelle ovviamente tutte con dimensione intorno al nanometro. La sigla HDPE (Hihg Density PolyEthilene) sicuramente non è nuova a chi abbia letto due cose sull'argomento Morgellons.
Le dimensioni sono state scelte come estremamente piccole (sostanzialmente con un fibra dello spessore del nm, possiamo infilzare una particella virale, come una cigliegia con un ago) appunto per minimizzare il fenomeno della separazione della scia in varie fasi. Insomma se spargiamo delle schifezze, ci dobbiamo assicurare che queste con il vento non si allontanino troppo dalla scia di vapore per non dare l'effetto a scia multi-stratificata che si vedrebbe da terra, e si mascherino bene tra le particelle di ghiaccio e di vapore. Come si vede appunto dal grafico, la dispersione è minima, anche se non nulla. Pertanto occorrono delle particelle non troppo grandi (altrimenti non rimarrebbero in aria per troppo poco tempo contrastando con l'ipotesi della durata eccessiva delle scie) nè troppo piccole (altrimenti se ne andrebbero in giro con il vento senza mai cadere a terra e provocando lo spiacevole e vistoso effetto della scia multi-stratificata). Come avremo modo di dimostrare però in seguito, risolvendo le equazioni di condensazione, queste dimensioni però stridono con l'ipotesi di rilevamento a terra di ingenti quantità di particelle nanometriche dopo tempi di permanenza in aria compatibili con l'ipotesi della grande durata delle scie chimiche (questo è dovuto al fatto che la condensazione e la flocculazione tendono a spostare a destra e comprimere la distribuzione di raggio delle particelle in funzione del loro numero con l'avanzare del tempo, facendo quindi sì che dopo un po' non si trovino quasi più particelle al di sotto di un certo diametro).
Nella prossima parte invece vedremo di condurre delle simulazioni più dettagliate considerando tutti i termini che compaiono nell'equazione e vedremo come fare ad impostare la risoluzione di un'equazione integro-differenziale che per giunta ha pure un kernel di integrazione assai brutto (guardate un po' che succede se tau è pari proprio a t, all'estremo superiore di integrazione).
Nota: nel mettere i dati prelevati dalla sonda nel modello, occorre fare attenzione alle unità di misura: la temperatura va convertita da [C°] in [K], l'umidità relativa va divisa per 100, la pressione e le altezze, non vanno modificate e possono essere usate tranquillamente nei modelli così come sono.
Le dimensioni sono state scelte come estremamente piccole (sostanzialmente con un fibra dello spessore del nm, possiamo infilzare una particella virale, come una cigliegia con un ago) appunto per minimizzare il fenomeno della separazione della scia in varie fasi. Insomma se spargiamo delle schifezze, ci dobbiamo assicurare che queste con il vento non si allontanino troppo dalla scia di vapore per non dare l'effetto a scia multi-stratificata che si vedrebbe da terra, e si mascherino bene tra le particelle di ghiaccio e di vapore. Come si vede appunto dal grafico, la dispersione è minima, anche se non nulla. Pertanto occorrono delle particelle non troppo grandi (altrimenti non rimarrebbero in aria per troppo poco tempo contrastando con l'ipotesi della durata eccessiva delle scie) nè troppo piccole (altrimenti se ne andrebbero in giro con il vento senza mai cadere a terra e provocando lo spiacevole e vistoso effetto della scia multi-stratificata). Come avremo modo di dimostrare però in seguito, risolvendo le equazioni di condensazione, queste dimensioni però stridono con l'ipotesi di rilevamento a terra di ingenti quantità di particelle nanometriche dopo tempi di permanenza in aria compatibili con l'ipotesi della grande durata delle scie chimiche (questo è dovuto al fatto che la condensazione e la flocculazione tendono a spostare a destra e comprimere la distribuzione di raggio delle particelle in funzione del loro numero con l'avanzare del tempo, facendo quindi sì che dopo un po' non si trovino quasi più particelle al di sotto di un certo diametro).
Nella prossima parte invece vedremo di condurre delle simulazioni più dettagliate considerando tutti i termini che compaiono nell'equazione e vedremo come fare ad impostare la risoluzione di un'equazione integro-differenziale che per giunta ha pure un kernel di integrazione assai brutto (guardate un po' che succede se tau è pari proprio a t, all'estremo superiore di integrazione).
Nota: nel mettere i dati prelevati dalla sonda nel modello, occorre fare attenzione alle unità di misura: la temperatura va convertita da [C°] in [K], l'umidità relativa va divisa per 100, la pressione e le altezze, non vanno modificate e possono essere usate tranquillamente nei modelli così come sono.
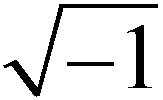

5 commenti:
Radau e Lobatto?Che cosa sono?!?!?!
Noi usavamo i vari ODE e Runge-Kutta ma questi non li conosco!Cosa hanno di differente?
Ottimo lavoro, sciaffaci su un copyleft!
Allora, hai presente i Runge Kutta classici ? Hai presente che la tabella di Butcher generalmente è praticamente una matrice "triangolare inferiore" (nel senso che la parte sopra è vuota e non ci sono numeri diversi da zero sulla diagonale) ?
Ecco, quei numeretti vengono derivati risolvendo dei sistemi di equazioni non lineari, eventualmente imponendo certi vincoli (ad esempio che la tabella di Butcher risultante dia luogo ad un metodo di Runge-Kutta con certe proprietà di stabilità, o che per esempio soddisfi dei vincoli sull'errore commesso in fase di integrazione). Queste equazioni si ricavano da schemi di approssimazione delle derivate e/o formule di quadratura (usate per l'approssimazione di integrali). Vedesi per esempio il metodo dei trapezi, che è alla base del metodo di integrazione di Heun (un passo di Eulero esplicito, e poi un'altro che ha tutta la forma del metodo dei trapezi). I metodi di Runge Kutta basati su Lobatto o Radau, sono metodi appunto che sfruttano le quadrture di Radau o di Lobatto. Ora la cosa figa è che sono dei metodi molto potenti (ci puoi integrare di tutto, anche equazioni brutte come quella di Van der Pol con mu sufficientemente basso, che basta per mandare in pappa qualunque metodo di integrazione esplicito), la fregatura è che a differenza dei metodi di Runge-Kutta classici, non basta calcolare la funzione in un punto noto per poterla calcolare, occorre risolvere un sistema di equazioni non lineari. Per esempio, per darti un'idea, il metodo di eulero esplicito è una roba del tipo
x(n+1)=x(n)+h*f(x(n),t(n))
l'eulero implicito invece è
x(n+1)=x(n)+h*f(x(n+1),t(n+1))
Ovviamente in questo caso per tirare fuori il valore di x(n+1) ti tocca risolverti un equazione (spesso non lineare). Stesse modalità nei metodi di Runge Kutta Impliciti basati su quadratura di Radau e Lobatto (che sono quelle un po' più famose). Questi ahimè non vengono quasi mai implementati all'interno di software commerciali (giusto il Mathematica, dove praticamente puoi costruirti tu un metodo di Runge-Kutta specificando direttamente la tabella di Butcher ed usare quel metodo per risolvere le tue equazioni differenziali). l'ode23tb (quello di matlab) per esempio usa una cosa simile all'eulero implicito. La cosa molto carina è in che questi metodi la precisione non è estremamente vincolata alla dimensione del passo di integrazione. Spero di essere stato esauriente, se dovessi avere altre curiosità o domande non esitare a chiedere.
P.s. ho trovato un modo per lavorarmi l'integrale bastando dell'equazione generale della dinamica della particella.
Caspita, certo!Chiaro!Non conoscevo questi metodi, noi ci siamo limitati a problemi assai più corti e complessi con gli ode,qualche volta con gli eulero.
Ora sono alle prese con shalstab...
Mah, guarda, quanto al risolutore da usare dipende un sacco dal problema. Ci sono problemi per cui per esempio sono meglio i metodi espliciti. Insomma non ha molto senso sparare con una bomba termonucleare ad una formica per ammazzarla, basta molto meno. Unica cosa è che qualche volta esce fuori un problema bastardo che non vuole saperne di farsi integrare dai risolutori espliciti, ed è in questi casi che ti tocca scrivere codice a mano, spulciare pubblicazioni etc ...
Tanto per farti un'esempio, la simulazione di sistemi non stazionari in genere crea un sacco di problemi. Insomma se provi ad integrare con metodi espliciti, quelle poche volte che il metodo converge e non si inchioda prima cominci a vedere oscillazioni anche dove non dovrebbero essercene. Mi è capitato in fase di progettazione di un controllo per una piattaforma di Stewart.
Shalstab ... sto dando un'occhiata, sembra una figata ! :D
Cuorenero, un consiglio: lascia perdere...
Ho seguito con molto interesse il tuo lavoro, ma, amenochè non sia soprattutto l'interesse personale a spingerti (e spero sia così), ti consiglierei di dedicare ad altro le tue energie... mi dispiace veramente vedere gente che spreca ancora il suo tempo e la sua preparazione per questa storia delle scie chimiche. Anche io quando, non molto tempo fa, ho scoperto la risonanza che aveva assunto questa faccenda sulla rete, sono rimasto basito, e sono stato tentato di darmi da fare... ma qui non si tratta più di sacche di ignoranza come dici tu, quanto di mancanza totale di senso critico e di buon senso tout court. E per questo credo non ci sia nulla da fare...
Pazienza dire che le scie (anche quelle di condensazione, perchè è così) possono avere una (risibile) influenza sul clima in quanto catalizzano la formazione di nubi; pazienza dire che i vertici militari dei paesi occidentali siano interessati alla modificazione e al controllo del clima come arma strategica e abbiano compiuto esperimenti in tale direzione, perchè è vero. Passi anche collegare le due cose e parlare di scie chimiche, magari rilasciate da aerei militari. Ma io vedo sempre più spesso gente che chiama "scia chimica" qualunque scia veda in cielo, e ad esse attribuisce qualunque fenomeno metereologico, dal rosso del cielo al tramonto, alla nebbia in inverno, al vento in primavera... Cosa pensi di poter fare con gente così priva di logica e senso critico e spirito di osservazione (se avessero veramente guardato il cielo prima che fosse straker a dirglielo...)? Tra l'altro qualunque cosa tu scriva va solo a vantaggio dei sostenitori della causa, perchè ormai sei stato tacciato come "disinformatore"... Avrai visto che sei apparso in buona compagnia in una lista di pericolosi occultatori della verità, in uno degli innumerevoli blog di straker e compagnia...
Di fronte alla tenacia di gente come straker, che pare non abbia null'altro da fare, è lecito dubitare che ci sia veramente un "complotto", qualcuno interessato a diffondere queste s*******e in modo da distogliere l'attenzione della gente dai problemi reali... L'unica cosa da fare secondo me sarebbe smettere di interessarsi di tutta la faccenda... questo è un appello anche per tutti gli altri debunkers che potrebbero leggere... Lasciamo cuocere gli sciachimisti nel loro brodo, forse prima o poi la cosa passerà da se come tutte le mode, quando la gente si renderà conto che non cambia mai nulla e che da anni si continuano a vedere sempre le stesse foto e filmati di presunte irrorazioni. Ma probabilmente continuare a "debunkare" non fa altro che alimentare l'attenzione sulla vicenda.
Posta un commento